Derivation of the Exposure Factor

The goal in close-up and macro photography is magnification of a subject. The technical process of achieving magnification is consequential for subject lighting and exposure. During the process of magnification, relative to infinity focus, there is a net loss of exposure density (defined as light intensity per unit area per unit time) at the film plane. Mathematically, this loss of exposure density is defined by the following relationship:

Net exposure density = exposure density lost (magnification) x exposure density gained (close focusing)  

                                                                                                                                                (Eq 1)

Once the net loss of exposure density is calculated, this value can be easily converted to an Exposure Factor that can be used to compensate for the exposure density loss. Essentially, this Exposure Factor tells us how many stops of exposure compensation (typically converted to a corrected shutter speed) are needed to achieve a proper exposure of a magnified subject.

To mathematically derive the net loss of exposure density, and thus the Exposure Factor, we will apply the time-honored Inverse Square Law and the classic thin lens model. 

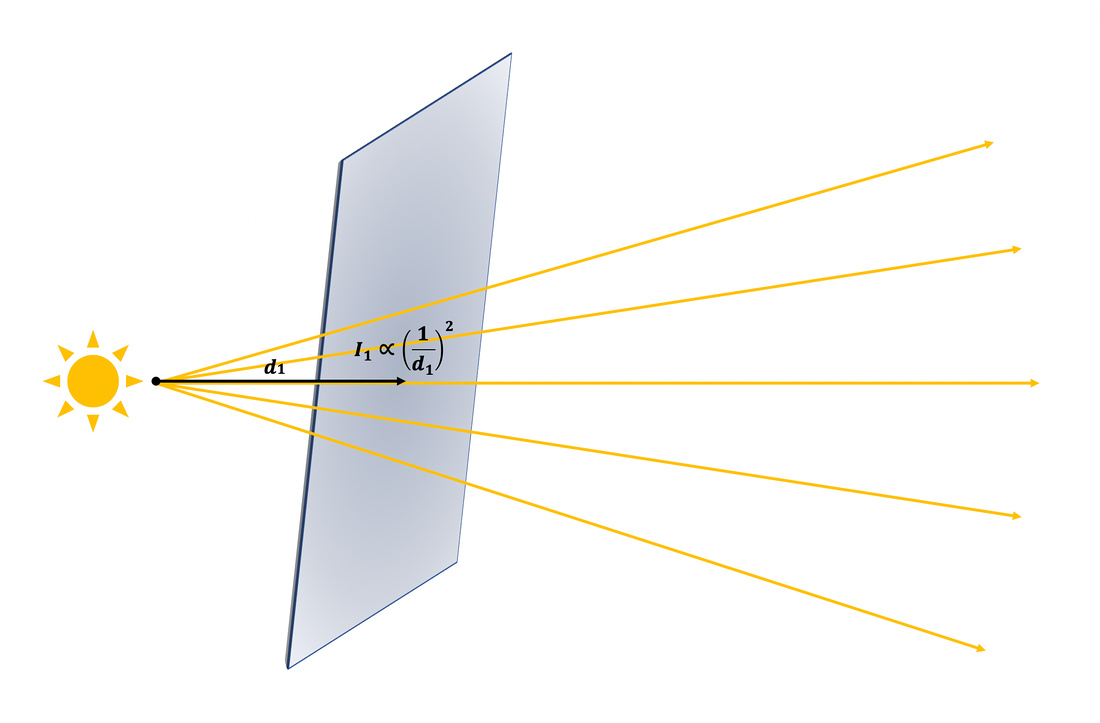
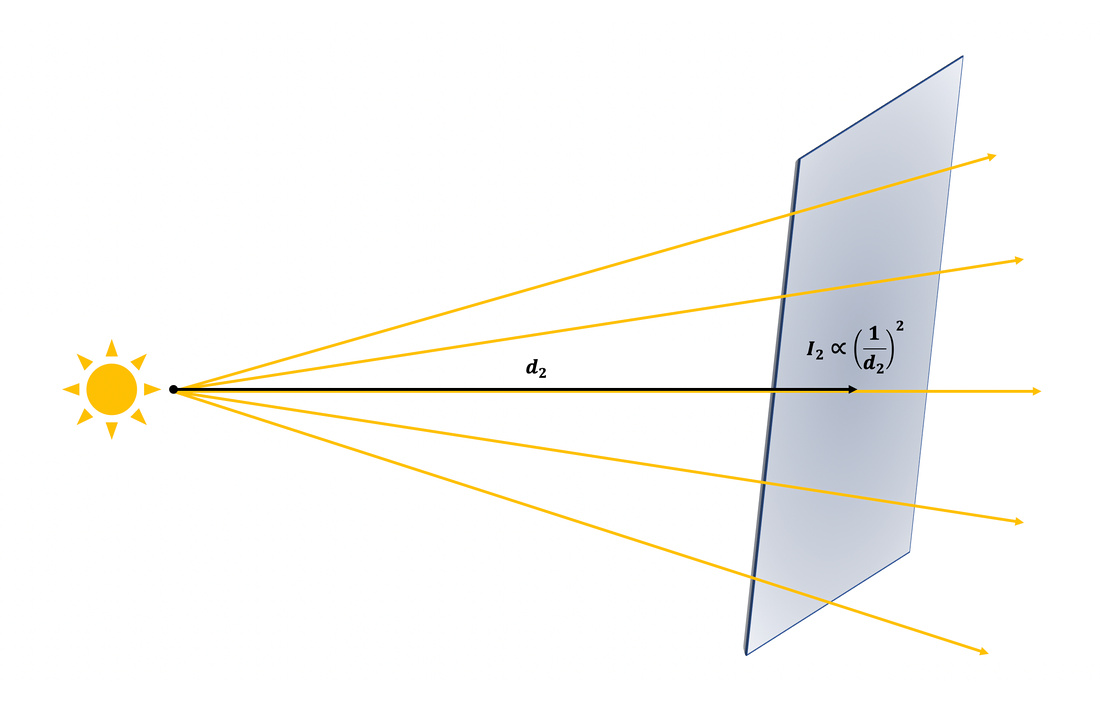
The Inverse Square Law: the intensity of light (energy per unit area) emanating from a point light source is inversely proportional to the square of the distance from the light source at that point in space and time.

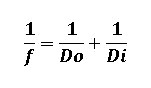
Thin Lens Equation
 

First, let’s derive the exposure density loss due to magnification (i.e., extending the lens from the film plane). Per the Inverse Square Law, in terms of the light traveling from the lens plane a distance Di to reach the film plane, the intensity of light striking the film plane before (I₁) and after (I₂) the lens is extended is given by the ratio:

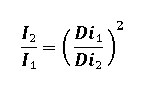
              (Eq 2)

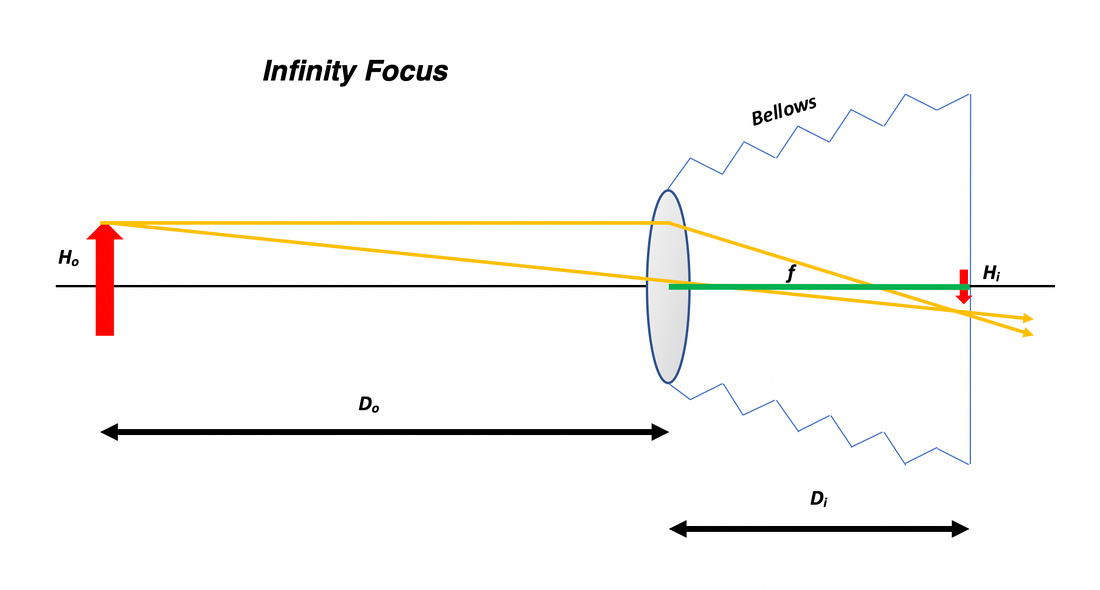
where Di₁ is the original distance between the image and lens plane and Di₂ is the new distance between the image and lens plane. In other words, Di₂ is the sum of the original image distance and the Extension of the lens from the film plane. From the basic lens diagram and the geometric law of similar triangles, the Magnification is given by:

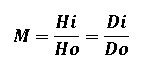
Thus, magnification is the ratio of the image height, H_i, on the film plane to the subject height, H_O. Intuitively, it should also make sense that the greater the distance between the image and lens plane (i.e., the more the lens is extended from the film plane) relative to infinity focus, the greater the magnification.

In this case, we are varying only the image distance (via lens extension) to achieve magnification; the subject distances -- before and after the lens is extended -- will remain constant. Rearranging the equation for magnification (in terms of the image and subject distances) followed by substitution into Equation 2 gives:

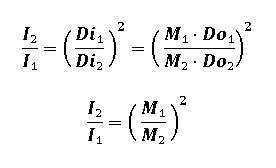
                                                                      (Eq 3)

Equation 3 represents the exposure density lost at the film plane due to magnification. Next, let’s derive the exposure density gained at the film plane due to close focusing (i.e., moving the camera/lens toward the subject). Per the Inverse Square Law, in terms of the light traveling from the subject a distance D_O to reach the lens plane, the intensity of light striking the film plane before (I₁) and after (I₂) the camera/lens is moved closer to the subject to achieve focus is given by the ratio:

                              (Eq 4)

Starting with the classic thin lens equation and applying algebraic manipulations, we eventually have:

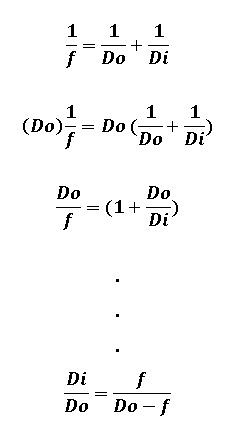
Since we know from above that magnification is the ratio of the image distance to subject distance, we have:

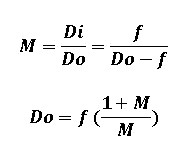
Next, substituting this new relationship for D_O into Equation 4 gives:

                                                             (Eq 5)

Equation 5 represents the exposure density gained at the film plane due to close focusing (i.e., decreasing the subject distance). Next, substituting both Equation 3 and Equation 5 into Equation 1, we have:

Screenshot

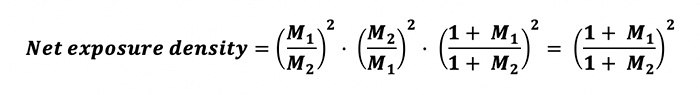
Since M₂ > M₁, the net exposure density is less than unity. Hence, there is net exposure density loss at the film plane. In the special case of starting off from zero magnification (i.e., infinity focus), M₁ is zero and we have:

Screenshot

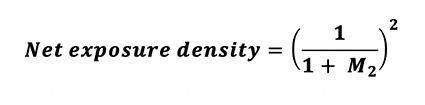
In order to neutralize this inevitable exposure density loss at the film plane and achieve a proper exposure of the magnified subject, this same factor -- converted to a reciprocal factor -- must be applied to the exposure indicated by the light meter in order to yield a corrected shutter speed. Hence, the Exposure Factor correction becomes:

Screenshot

Screenshot

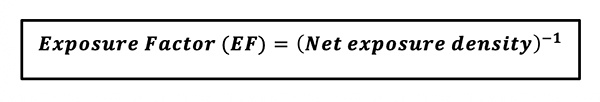
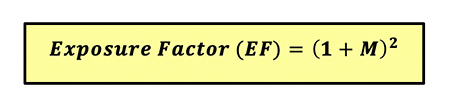
                                                                                                                                  (Eq 6)
 

To derive relationships for the Exposure Factor and Magnification expressed in terms of the extension (or bellows), we start with the thin lens equation:

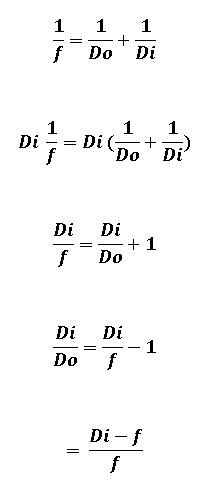
The expression for magnification then becomes:

Based on the thin lens model the image distance, D_i, equals the focal length, f, when the lens is focused at infinity. By definition, magnification occurs when the lens is extended beyond infinity focus. The difference between D_i and the focal length equals the extension, EXT, of the lens past infinity focus. Therefore, the magnification can be expressed as:

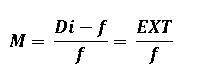
The salient feature of this expression is that magnification is directly proportional to the lens extension in use:

Intuitively, what this expression tells us is that by enabling the light to travel farther between the lens and the image plane, the projected image circle will enlarge, which is also a consequence of the Inverse Square Law.

In the case of a camera using solely a bellows attachment directly between the film plane and the lens, we know that when the lens is focused at infinity, by definition the bellows length equals the focal length. Subsequently, when the lens is extended from infinity to magnify, the bellows length is the sum of the focal length and the extension of the lens past infinity focus: B = EXT + f. With additional algebra, the magnification becomes:

Expressed in terms of the bellows length, with additional algebraic manipulations the Exposure Factor correction (Equation 6) becomes:

Screenshot

Screenshot

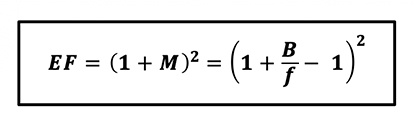
Intuitively, what this expression tells us is that by enabling the light to travel farther between the lens and the image plane to form an enlarged image circle (i.e., magnification), the exposure density loss to be compensated varies with the square of that distance (i.e., the extension). Mathematically, these concepts can be simplified further to:

Screenshot

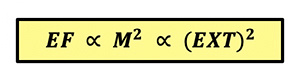
In summary, in macro photography exposure density loss at the image plane is governed by the Inverse Square Law.

Derivation of the Subject-Lens Distance Threshold for Exposure Compensation

Rule of thumb: the threshold lens-subject distance at and within which exposure compensation must be applied for exposure density loss due to magnification corresponds to a minimum distance of nine focal lengths. If the lens-subject distance is exactly nine focal lengths, an exposure compensation of +⅓ stops of light must be applied.

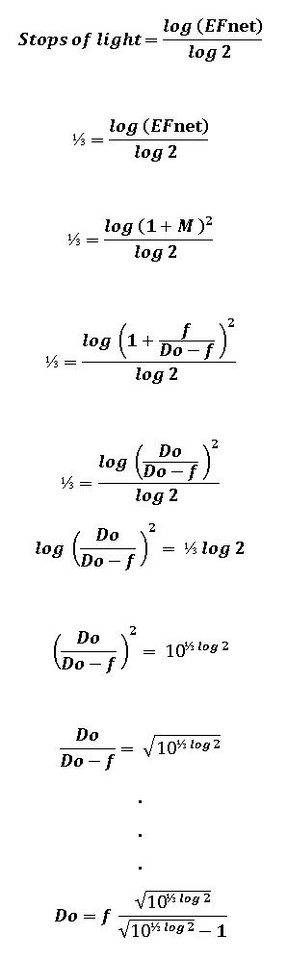
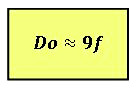
A subject distance of 9 focal lengths corresponds to a magnification of:

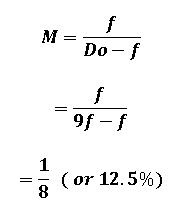
Of course, at a subject distance of twice the focal length, the magnification will be 1:1 (100%), and the exposure compensation will be +2 stops of light.

Derivation of the “Effective F-stop"

By definition, the physical size of the aperture equals the ratio of the focal length to the F-stop. Let f₁ be the focal length at infinity focus and f₂ the "effective focal length" -- the sum of the focal length at infinity and the extension of the lens from infinity focus. Similarly, let F-stop₁ be the F-stop at infinity (i.e., the "working F-stop") and F-stop₂  be the "effective F-stop" at the point of lens extension: 

In the special case of a 1:1 magnification where by definition two stops of exposure density (light intensity per unit area) are lost at the film plane, the “effective F-stop” is equal to twice the working F-stop:

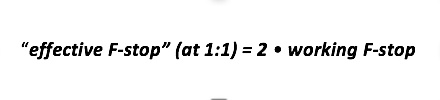
Thus, a working F-stop of f/16 used to make an exposure at 1:1 behaves “as if” the real F-stop were f/32, since two stops of exposure density are lost at the film plane; yet the actual physical size of the aperture is unchanged and the total quantity of light exposing the film per unit time is also unchanged.

This is a salient conceptual point: all things being equal, compared to infinity focus there is no absolute change in the exposure when a subject is magnified. But, there is a loss of exposure density (light intensity per unit area per unit time), because the same quantity of light that enters the lens at infinity focus is now spread out over an enlarged image circle as the light travels farther from the lens to reach the film plane. This is the essence of the Inverse Square Law. 

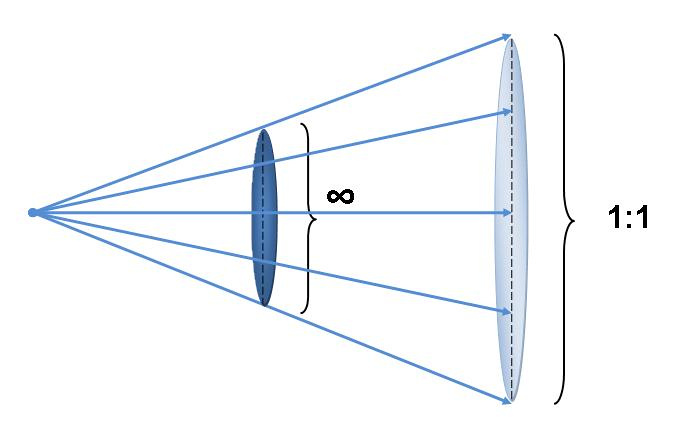
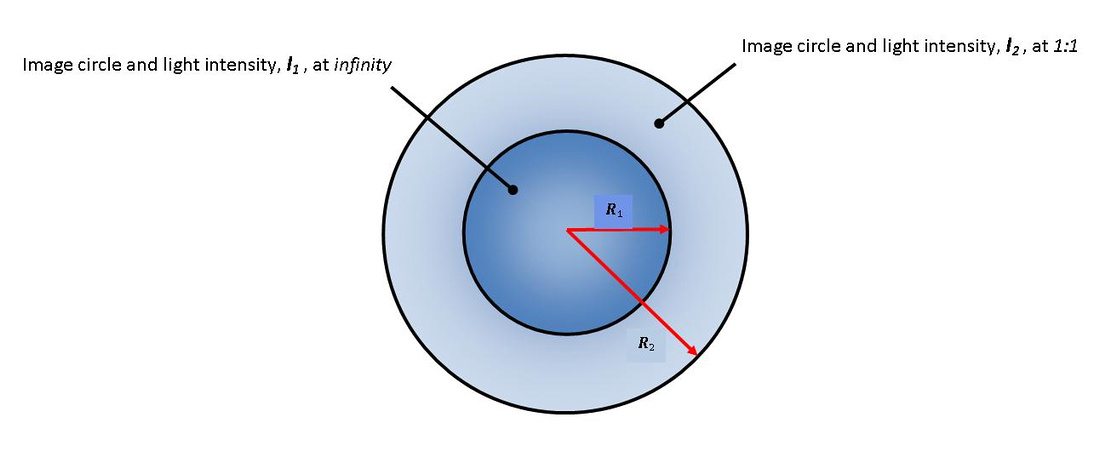
In the special case of a 1:1 magnification, the same exposure at infinity focus is now spread out over an image circle that is twice in diameter and four times larger in surface area. Hence, the ¼ loss of exposure density at 1:1. For pedagogical purposes, this may be conceptualized as conservation of energy. That is to say, for a given quantity of energy (i.e., visible light radiation) that is transmitted to the film plane at infinity focus, if the illuminated surface area of the film plane enlarges by a factor of four, then the energy per unit area must drop by a factor of ¼.

The identical exposure (i.e., equivalent scene luminance, aperture, and shutter speed) at infinity focus (left panel) and at 100% magnification (right panel). Note the markedly disparate exposure densities.

If the photographer chooses to use an “effective F-stop” to calculate Exposure Factor, then this “effective F-stop” can be used on the light meter to determine the corrected shutter speed to make a proper exposure.

For example, if the spot light meter gives an EV of 9.0 at f/16 with ISO 100 film, then the shutter speed would be ½ second. Multiplying this shutter speed by the Exposure Factor, 4x (or two stops), gives a corrected shutter speed of 2 seconds at a 1:1 magnification. Alternatively, if the photographer sets an “effective aperture” of f/32 on the light meter, then the corrected shutter speed is read off directly from the meter as 2 seconds.

Further, in terms of the “effective focal length”, the focal length during magnification behaves “as if” it were increased by an amount equivalent to the lens extension. That is,

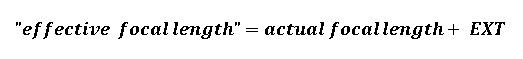
For example, at 1:1 magnification a lens with a focal length of 150 mm behaves “as if” it has an actual focal length of 300 mm, since the lens must be extended by 150 mm to create a 100% magnification. Thus, since light must travel twice the distance to reach the film plane compared to infinity focus at 150 mm, the Inverse Square Law dictates that the light intensity per unit area exposing the film is reduced by ¼, or two stops of light.

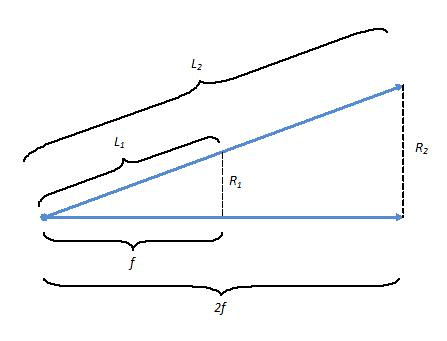
By the Inverse Square Law,

By similar triangles,

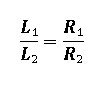
The Inverse Square Law becomes:

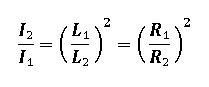
By definition, at 1:1 magnification the exposure density (light intensity per unit area) at the film plane is reduced by ¼. The relationship then becomes:

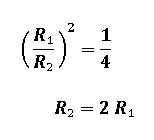
Thus, at 1:1 the diameter of the image circle doubles.

If the photographer prefers to work at a set “working distance” (closely approximated by the subject-lens distance) and does not wish to compromise this distance for technical or aesthetic reasons, then more magnification can be attained by simply using a lens of a longer focal length, provided of course, the photographer has the means to increase the lens extension. Mathematically, this is shown by the following relation:

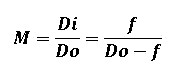
At a fixed subject distance (working distance), the magnification can be increased with a longer focal length. But to obey the thin lens equation, the image distance, D_i (i.e., lens extension), must also be increased.

Alternatively, if the photographer has a limited amount of lens extension with which to work but does not care about the working distance, then increasing magnification can be achieved by using a lens of a shorter focal length, but this of course would involve moving the lens even closer to the subject. Mathematically, this is shown by the following relation:

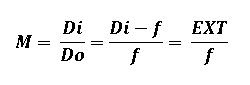
At a fixed lens extension, the magnification can be increased with a shorter focal length. But to obey the thin lens equation, the subject distance, D_o (working distance), must also be decreased.